25 Most Important Equations in the World
Published 11/10/24 - Alex
Math is a very important subject as it allows us to create a langauge in a sense for science, something that helps us explain the natrual world and things in our society
If you've read more of my articles in lessons im sure you know how much I stress this point! Math is important. And today were going to be showimg that by taking a look at some of the most influential, useful, and important equations ever discovered. We will list them in order of discovery date
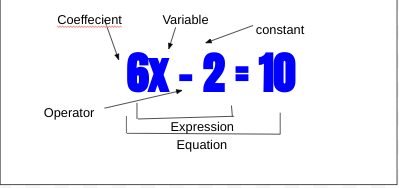
First of all lets make sure we know what an equation is its simply something that states two things are equal or have a connection or relationship between them
Equation #1 - Pythagorean Theorem - 1800 BC Babylonians and Egyptians, Pythagoras 530 BC in Greece
a2 + b2 = c2

The pythagorean theorem states that if you have any right triangle or a triangle with 90 degrees in the cornor made by 2 perpendicular lines then the two shortest sides times themselves will be equal to the largest side times itself. This very basic geometric theorem is the foundation for all of trigonometry, geometry and solving many, many problems within out world! Although named after the greek mathematician Pythagoras this was known by many ancient civilizations such as the Babylonians, Egyptians, Indians, and Chinese
Equation #2 - Chinese Remainder Theorem - Discovered by Sunzi 300 BC in China

This formula was first used by the chinese to develop accurate and detailed calendars although it is quite useful for many modern applications such as Number Theory Proofs, Efficiency in computation, and cybersecurity
Equation #3 - Binomial Theorem / Pascal's Triangle - Discovered by Jia Xian in China and Omar Khayyam in Persia (Iran) 1000s
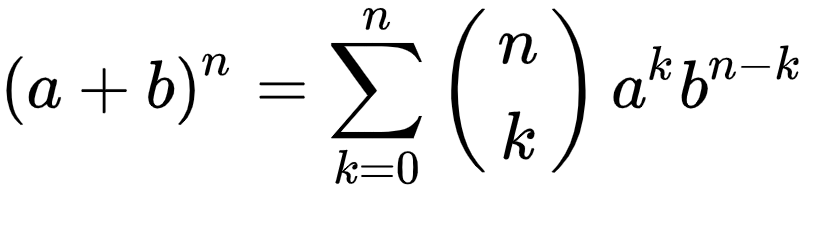
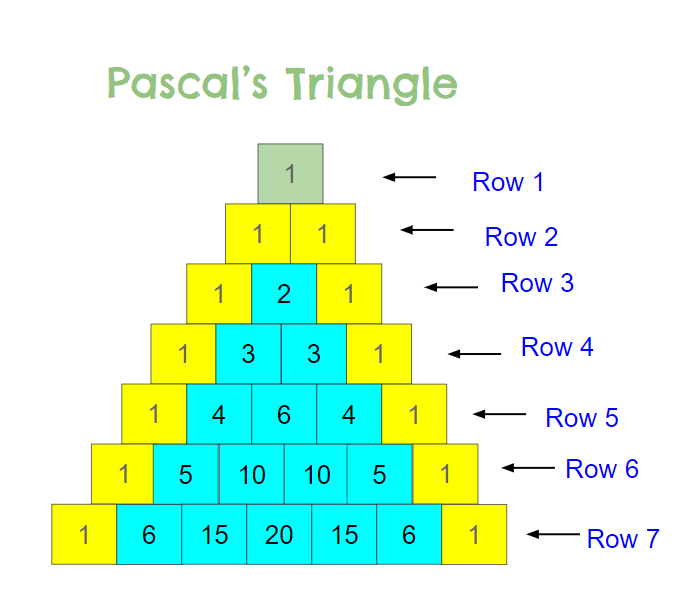
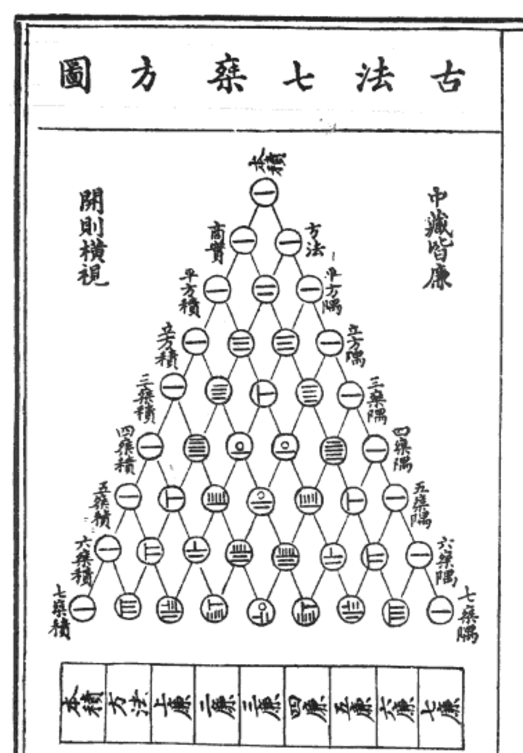
A very important series of patterns in math that has many applications in algebra and arithmetic. The associated uses are very important in statistics, probability, and combinatronics as well as finance
Equation #4 - Logarithmic Product Rule - John Napier 1610 Scotland

This very important logarithm rule thought to be discovered by John Napier in 1610 is very important for solving a number of problems related to exponents and exponential growth as well as establishing how we can break expressions up from multiplication to addition
Equation #5 - Fundimental Theorem of Calculus - Discovered by James Gregory 1667 in Scotland
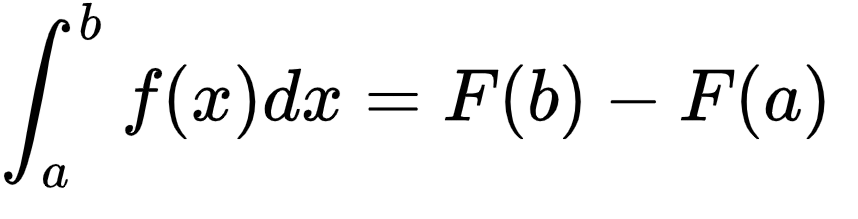
Calculus is one of the most important feilds of mathematics and all modern science and engineering is built on the foundations of calculus which considers the study of the changing world. The fundimental theorem states a relationship between the derrivite and integral of a function
Equation #6 - Compound Interest - Discovered by Jacob Bernoulli 1683 in Switzerland
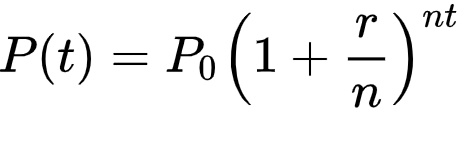
Compound interest is very important in the modern financial world and also lead to the discover of Euler's Number e which is one of the most important constants in all of mathematics
Equation #7 - Second Law of Motion - Isaac Newton 1687 in England

Establishes the fact that forces are responsible for motion. This equation was responsible for the birth of modern physics and are understanding of the world from describing the movements of astronomical bodies to things that happen on earth
Equation #8 - Law of Gravity - Isaac Newton 1687 in England

Gravity is the most fundimental force that holds our universe together so much that many physicists like Einstein belive that it is not even a force instead just the way the universe behaves for reasons we will not cover in this, however this law states the important fact that every single particle in the universe attracts every other with force proportional to thier masses multiplied and is also inversly proportional to the square of the distance seperating them
Equation #9 - Taylor's Theorem - Brook Taylor 1712 in England

Very important theorem side by side with the fundimental theorem of calculus. This allows us to study analyticity of functions and approxmate things in physics, engineering and more. In simple terms this lets us understand an arithmatic sequence that up to infinity appromates functions such as exponential and trigonometric ones both of which are crucial in math and science
Equation #10 - Wave Equation - Jean le Rond d’Alembert 1746 in France
